Трёхдиагональная матрица

Текущая версия (не проверялась)

Трёхдиагональной матрицей называют матрицу следующего вида:

.

Системы линейных алгебраических уравнений с такими матрицами встречаются при решении многих задач математики и физики. Краевые условия x1 и xn, которые берутся из контекста задачи, задают первую и последнюю строки. Так краевое условие первого рода F(x = x1) = F1 определит перую строку в виде C1 = 1, B1 = 0, а условие второго рода dF / dx(x = x1) = F1 будет соответствовать значениям C1 = − 1, B1 = 1.

Метод прогонки

Для решения систем вида используется метод прогонки, основанный на предположении, что искомые неизвестные связаны рекуррентным соотношением:

     , где                                      (1)

Используя это соотношение, выразим xi-1 и xi через xi+1 и подставим в i-e уравнение:

,

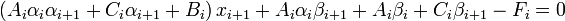где Fi - правая часть i-го уравнения. Это соотношение будет выполняться независимо от решения, если потребовать

Отсюда следует:

Из первого уравнения получим:

. .

После нахождения прогоночных коэффициентов α и β, используя уравнение (1), получим решение системы. При этом,

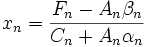
Ссылки

Алгоритм метода прогонки
Костомаров Д.П., Фаворский А.П. "Вводные лекции по численным методам"