Текущая версия (не проверялась)
Текущая версия (не проверялась) | Битва при Хлеву | |||||
|---|---|---|---|---|---|
| |||||
| Стороны | |||||
| тархистанцы | нарнийцы | ||||
| Командующие | |||||
| Ришда | Тириан | ||||
| Силы сторон | |||||
| 15 псов, единороги, медведи, кабаны, 3 людей, мыши, кроты, 2 белки | |||||
| Потери | |||||
| После 1 этапа:З тархистанца, 1 лис, 1 бык | После 1 этапа:3 пса, 1 медведь | ||||
Битва при Хлеву - последнее в истории Нарнии сражение, о котором рассказывается в седьмой книге «Хроник Нарнии» - «Последней битве».
Битва
Первый этапТархистанский главнокомандующий Ришда приказал живьём хватать и бросать в Хлев нарнийцев. Тархистанцы двинулись на нарнийцев, и завязалась битва.
Второй этапЗа время перерыва между двумя этапам, гномы, которые сражались за себя, перестреляли всех коней.Тем временем вдалеке раздался барабан - к тархистанцам шло подкрепление. Король Тириан решил атаковать до того, как прибкдет подкрепление. Джил и орёл Дальнозор отвлекали врагов, а потом нарнийцы неожиданно пошли на тархистанцев. Вскоре подкрепление дошло до тархистанцев, и Тириан дал приказ отступать.
Бой тархистанцев и гномов Третий этапРишда обьявил, что если кабан, собаки и единорог сдадутся, он оставит им жизнь, но продаст их в рабство.В ответ раздалось грозное рычание, и Ришда приказал убить зверей, а людей взять живыми.
Так начался третий и последний этап битвы при Хлеву.Надежды на победу у нарнийцев не было, потому что у тархистанцев были копья.Неожиданно на поле битвы появилась Таш, и сражение прекратилось.


 Интерьер
Интерьер 

 .
.  используется метод прогонки, основанный на предположении, что искомые неизвестные связаны рекуррентным соотношением:
используется метод прогонки, основанный на предположении, что искомые неизвестные связаны рекуррентным соотношением: , где
, где  (1)
(1) 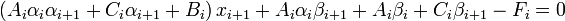 ,
, 



 .
.  .
.