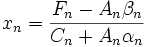Текущая версия (не проверялась)
| Владимир Дмитриевич Коссинский |
| 6 сентября 1830 — 22 января 1889 |
генерал-лейтенант Владимир Дмитриевич Коссинский |
| Место смерти | Санкт-Петербург |
| Принадлежность |  Россия |
| Род войск | пехота |
| Звание | генерал-лейтенант |
| Сражения/войны | Крымская война, Русско-турецкая война 1877—1878 |
| Награды | Орден Святой Анны 3-й ст. (1855), Орден Святого Владимира 4-й ст. (1869), Орден Святого Станислава 1-й ст. (1874), Орден Святой Анны 2-й ст. (1877), Орден Святой Анны 1-й ст. (1877), Орден Святого Владимира 2-й ст. (1878). |
Владимир Дмитриевич Коссинский (Косинский) (1830—1889) — русский генерал, участник русско-турецкой войны 1877—1878 гг.
Родился 6 сентября 1830 г., происходил из дворян Полтавской губернии, воспитывался во 2-м кадетском корпусе, 29 мая 1849 г. был произведён в прапорщики с назначением в Лейб-гвардии Литовский полк. В апреле 1854 г. Коссинский пожелал перейти в действующую против англо-французов армию и был переведён в Могилёвский пехотный полк с переименованием в капитаны. С 1 мая по 27 августа 1855 г. он находился в Севастопольском гарнизоне, 14 мая был на 4-м бастионе сильно контужен; за отличие был награждён орденом св. Анны 3-й степени). По окончании военных действий Коссинский был снова переведён в гвардию; в 1861 г. был делопроизводителем Высочайше учрежденного комитета для определения довольствия армейских войск; эти труды послужили основой для составления «Заметки по поводу предполагаемого преобразования нынешней системы продовольствия войск» (СПб., 1866). Затем Коссинский был назначен помощником делопроизводителя концессии для улучшений по военной части, в марте 1863 г. помощником правителя дел специального комитета по устройству и образованию войск. В апреле 1867 г. Коссинский был назначен делопроизводителем канцелярии военного министра и вместе с тем состоял членом комиссии по образованию офицерских собраний, устройству военных библиотек и в комиссии по пересмотру законоположений о чинопроизводстве в войсках.
17 апреля 1870 г. он был произведён в генерал-майоры (старшинство с 1 января 1872 г.). В 1872 г. Коссинский был назначен председателем комиссии, назначенной для осмотра военно-исправительных рот; в течение 1873 и 1874 гг. был председателем особой комиссии для пересмотра хозяйства Медико-хирургической академии и в то же время состоял членом комиссии для пересмотра правил о порядке представлений к наградам и комиссии для разработки правил относительно назначения подъемных и путевых пособий лицам, командируемым за границу, а также в комиссии для распределения пособий. По объявлении в 1877 г. войны Турции он был назначен инспектором госпиталей действующей армии в Европейской Турции. Участвовал в отражении турок на Шипкинском перевале и был награждён орденами св. Владимира 2-й степени с мечами и св. Анны 2-й степени с мечами.
Заболев тифом, Коссинский принужден был возвратиться в Петербург. Оправившись от болезни он был назначен членом Главного военно-госпитального комитета, в 1880 г. осматривал госпитали и лазареты на Кавказе, в 1881 г. принимал деятельное участие в организации военного обоза, в 1882 г. в разработке положений об окружных и корпусных управлениях, в 1883 г. был председателем комиссии для рассмотрения вопроса о способе содержания Кавказских минеральных вод и определения новых условий для пользования ими больных воинских чинов. 15 мая 1883 г. произведён в генерал-лейтенанты.
С 1869 г. В. Д. Коссинский состоял членом комитета по устройству Севастопольского музея и был его казначеем, а также одним из главных распорядителей. Он написал стихотворные «Севастопольские былины» (СПб., 1867; 2-е доп. изд.: СПб., 1874), в которых изложил эпизоды боевой жизни в 1855 г.; печатал свои статьи по разным специально-военным вопросам в военных периодических изданиях; особенно важен его труд, составленный по поручению военного министра — «Систематический сборник приказов по военному ведомству и циркуляров Главного Штаба» (СПб., 1887).
Умер 22 января 1889 г. в Петербурге.
Текущая версия (не проверялась) 
Текущая версия (не проверялась) 
Текущая версия (не проверялась) 
Текущая версия (не проверялась) 
Интерьер 
. 
используется метод прогонки, основанный на предположении, что искомые неизвестные связаны рекуррентным соотношением:
, где 
(1) 
, 
. 
. 
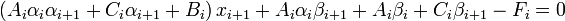